Ing.Alessandro Tasora

Università di Parma
Dipartimento di Ingegneria Industriale

• Home
• Università di Parma

Mechanical simulation of multibody systems with friction and contacts on GPU boards, using CUDA

Italian team	Alessandro Tasora (Università degli Studi di Parma)
USA team	Dan Negrut, T.D. Heyn, J.C. Madsen, H.Mazhar et al. (University of Wisconsin, Madison); Mihai Anitescu (ANL).
Sponsor	NVIDIA Corporation, USA
Status	Almost completed, needs some optimizations
Year	From 2007 to present..

This research project is jointly developed by Prof. Alessandro Tasora at the University of Parma and by Prof. Dan Negrut and his SBEL Labs team at the University of Wisconsin.

Our goal is the development of a numerical method for simulating mechanical systems with millions of parts with joints, contacts, friction, forces, motors, etc. Thank to the adoption of the CUDA GPU technology from NVIDIA, the proposed method has been parallelyzed and now can perform the analysis of extremely complex systems such as granular material flows and off-road vehicle dynamics.



Above, some of our GPU boards, kindly donated by NVIDIA Corporation.

The development of parallel algorithms for simulation-based science and engineering has represented one of the most complex challenges in the field of numerical computing. Until recently the massive computational power of parallel supercomputers has been available to a relatively small number of research groups in a select number of research facilities, thus limiting the number of applications approached and the impact of high performance computing. This scenario is rapidly changing due to a trend set by general-purpose computing on the graphics processing unit (GPU). The CUDA libraries from NVIDIA allow one to use the streaming microprocessors mounted in high-end graphics cards as general-purpose computing hardware, easily achieving 1 TeraFLOP and more.

Our method is based on a time-stepping formulation that solves, at every step, a second-order cone constrained optimization problem. This time-stepping scheme, developed together with Mihai Anitescu from the MCS division at the Argonne National Laboratories USA, converges in a measure differential inclusion sense to the solution of the original continuous-time differential-variational inequality.





Above, an example of a granular problem: the simulation of a size segregation shaker (click on the picture to see the animation)





Above: in this benchmark (2009) H.Mazhar used the GPU-enabled Chrono::Engine to simulate two granular materials being mixed in a box that shakes horizontally.
The most intensive computational phase in the multibody simulation is the solution of the complementarity problem, that is the process that computes unknown speeds/accelerations and impulses/forces at a given time. We developed a matrix-less iterative solver that can exploit well the sparsity of the system and we ported it on the parallel GPU hardware. In the proposed approach, the data structures on the GPU are implemented as large arrays (buffers) to match the execution model associated with NVIDIA’s CUDA. Specifically, threads are grouped in rectangular thread blocks, and thread blocks are arranged in rectangular grids. Four main buffers are used: the contacts buffer, the constraints buffer, the reduction buffer, and the bodies buffer. Some of them are depicted below.


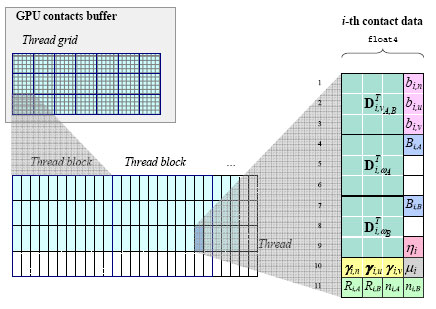
Above: each contact between two bodies is represented by this compact array in the GPU hardware

Note that our solver can also handle bilateral constraints, such as those introduced by usual mechanical joints (for example, revolute joints, spherical joints, prismatic guides, motors, and so on.)
The iterative solver requires a number of iterations to achieve convergence, and each iteration is performed as a quick sequence of few kernels, that are GPU parallel operations on the buffers. Among these kernels, the most important is the one that computes deltas in the body speeds. Since it may happen that two contacts need to apply some delta to the same body, we avoid these parallel-write-conflicts by using a custom reduction buffer as an intermediate structure, followed by reduction kernels.


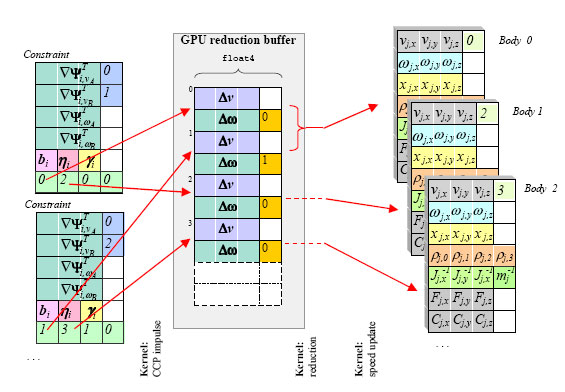
Above: a very basic sketch explaining the idea behind the reduction buffer.


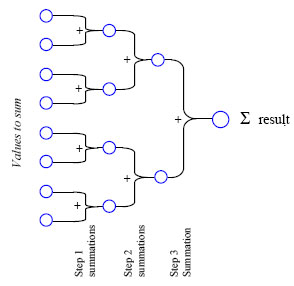
Above: multiple deltas applied to the same body are summed to a single effect by using a reduction kernel that works as a binary tree, to exploit the parallel architecture at its best.

Note that not all of the multibody simulation has been ported on the GPU. In particular, this is the case of the collision detection engine, which is still executed on the CPU and becomes the bottleneck of the entire simulation.


The method has been tested on different models of NVIDIA boards; the results that we discuss here are obtained with a simple 8800 GT board (we are studying how to exploit the double processor on the 9800 GX2 and how to use multiple GPUs on a single bus).

As a benchmark, we simulated 8'000 rigid spherical objects falling into a box. This leads, on average, to a complementarity system with more than 150'000 unknowns, to be solved at each time step.



Above: benchmark with 8'000 spheres stacking into a box (8x speedup in the complementarity problem)

We obtained, on average, a speedup of 8x when compared to an highly optimized CPU solver. Note that, as shown in the table below, the GPU solver spends only 1/3 of the time with parallel computation (the kernels are executed really fast), while the remaining 2/3 of the time is spent in doing bookkeeping for uploading the buffers from the CPU to the GPU, and viceversa. For this reason we foresee that even larger speedups can be achieved in future if we manage to reduce the overhead of data transfer between the CPU and the GPU.

	CPU (Pentium 3.5 GHz )	GPU (NVidia 8800 GT)
		kernels only GPU+CPU 48 ms 149 ms
Time [milliseconds] for 20 iterations	1150 ms

Currently we are performing other kinds of benchmarks, even including motors and bilateral joints, and the overall speedup is about one order of magnitude when compared to a plain CPU implementation. The speedup is appreciable only if the complexity of the system is high (for simple systems, with less than 1'000 rigid bodies, it is still faster to use the CPU serial solver).
A recent large scale benchmark (granular flow inside a nuclear reactor) showed a 13x speedup.

The development and the optimization of the solver will allow us to perform the simulation of massive multibody systems that has never been attacked with personal computers. In detail, we are interested in simulating:

• vehicles with tyres on granular soils;
• earth-moving machines with tracks, whose blades move sand & pebbles;
• granular flow in IV generation nuclear reactors of PBR type.

Above: example of granular flow in a 2D hopper (benchmark, 50'000 spheres)



Latest news! H.Mazhar won the 2009 ASME Student Competition! He implemented a GPU-based collision algorithm that, once merged with the Chrono::Engine solver, was used to simulate one million of bodies (above). The average speedup was more than 20x.

Interested people can find detailed informations here: